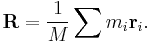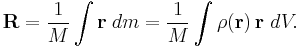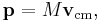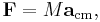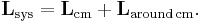Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body. In the case of a loose distribution of masses in free space, such as shot from a shotgun or the planets of the Solar System, the position of the center of mass is a point in space among them that may not correspond to the position of any individual mass.
The use of the mass center often allows the use of simplified equations of motion, and it is a convenient reference point for many other calculations in physics, such as angular momentum or the moment of inertia. In many applications, such as orbital mechanics, objects can be replaced by point masses located at their mass centers for the purposes of analysis. The center of mass frame is an inertial frame in which the center of mass of a system is at rest at the origin of the coordinate system.
In a uniform gravitational field, such as for small bodies near the surface of Earth, the weight of a body acts as if it were concentrated at the center of mass. For this reason, the center of mass is also called the center of gravity. Where gravity is not uniform, there can be a gravitational torque acting on objects. In some situations, this torque can be explained as arising from a generalized center of gravity that is distinct from the center of mass.
The center of mass of a body does not generally coincide with its geometric center, and this property can be exploited. Engineers try to design a sports car's center of mass as low as possible to make the car handle better. When high jumpers perform a "Fosbury Flop", they bend their body in such a way that it clears the bar while its center of mass does not.[1]
Contents |
Definition
The center of mass 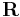 of a system of particles of total mass
of a system of particles of total mass  is defined as the average of their positions,
is defined as the average of their positions, 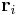 , weighted by their masses,
, weighted by their masses, 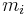 :[2]
:[2]
For a continuous distribution with mass density 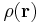 , the sum becomes an integral:[3]
, the sum becomes an integral:[3]
If an object has uniform density then its center of mass is the same as the centroid of its shape.[4]
Examples
- The center of mass of a two-particle system lies on the line connecting the particles (or, more precisely, their individual centers of mass). The center of mass is closer to the more massive object; for details, see below.
- The center of mass of a uniform ring is at the center of the ring; outside the material that makes up the ring.
- The center of mass of a uniform solid triangle lies on all three medians and therefore at the centroid, which is also the average of the three vertices.
- The center of mass of a uniform rectangle is at the intersection of the two diagonals.
- In a spherically symmetric body, the center of mass is at the geometric center.[5] This approximately applies to the Earth: the density varies considerably, but it mainly depends on depth and less on the latitude and longitude coordinates.
More generally, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.[6]
Properties
Momentum
For any system with no external forces, the center of mass moves with constant velocity. This applies for all systems with classical internal forces, including magnetic fields, electric fields, chemical reactions, and so on. More formally, this is true for any internal forces that satisfy Newton's Third Law.[2]
The total momentum for any system of particles is given by
where M indicates the total mass, and vcm is the velocity of the center of mass.[7] This velocity can be computed by taking the time derivative of the position of the center of mass. An analogue to Newton's Second Law is
where F indicates the sum of all external forces on the system, and acm indicates the acceleration of the center of mass. It is this principle that gives precise expression to the intuitive notion that the system as a whole behaves like a mass of M placed at R.[2]
The angular momentum vector for a system is equal to the angular momentum of all the particles around the center of mass, plus the angular momentum of the center of mass, as if it were a single particle of mass  :[8]
:[8]
This is a corollary of the parallel axis theorem.[9]
Gravity
The center of mass is often called the center of gravity because any uniform gravitational field g acts on a system as if the mass M of the system were concentrated at the center of mass R. Specifically, the gravitational potential energy is equal to the potential energy of a point mass M at R,[10] and the gravitational torque is equal to the torque of a force Mg acting at R.[6]
If the gravitational field acting on a body is not uniform, then the center of mass does not necessarily exhibit these convenient properties concerning gravity. A non-uniform gravitational field can produce a torque on an object about its center of mass, causing it to rotate.[6] The center of gravity seeks to model the gravitational torque as a resultant force at a point. Such a point may not exist, and if it exists, it is not unique. When a unique center of gravity can be defined, its location depends on the external field, so its motion is harder to determine than the motion of the center of mass; this problem limits its usefulness in applications.[11]
History
The concept of center of mass was first introduced by the ancient Greek physicist, mathematician, and engineer Archimedes of Syracuse. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point — their center of mass. In work on floating bodies he demonstrated that the orientation of a floating object is the one that makes its center of mass as low as possible. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes.[12]
Later mathematicians who developed the theory of the center of mass include Pappus of Alexandria, Guido Ubaldi, Francesco Maurolico,[13] Federico Commandino,[14] Simon Stevin,[15] Luca Valerio,[16] Jean-Charles de la Faille, Paul Guldin,[17] John Wallis, Louis Carré, Pierre Varignon, and Alexis Clairaut.[18]
Newton's second law is reformulated with respect to the center of mass in Euler's first law.[19]
Locating the center of mass
An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass.[20]
The shape of an object might already be mathematically determined, but it may be too complex to use a known formula. In this case, one can subdivide the complex shape into simpler, more elementary shapes, whose centers of mass are easy to find. If the total mass and center of mass can be determined for each area, then the center of mass of the whole is the weighted average of the centers.[21] This method can even work for objects with holes, which can be accounted for as negative masses.[22]
A direct development of the planimeter known as an integraph, or integerometer, can be used to establish the position of the centroid or center of mass of an irregular two-dimensional shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to ensure the ship would not capsize.[23]
Applications
Aeronautics
The center of mass is an important point on an aircraft, which significantly affects the stability of the aircraft. To ensure the aircraft is stable enough to be safe to fly, the center of mass must fall within specified limits. If the center of mass is ahead of the forward limit, the aircraft will be less maneuverable, possibly to the point of being unable to rotate for takeoff or flare for landing.[24] If the center of mass is behind the aft limit, the aircraft will be more maneuverable, but also less stable, and possibly so unstable that it is impossible to fly. The moment arm of the elevator will also be reduced, which makes it more difficult to recover from a stalled condition.[25]
For helicopters in hover, the center of mass is always directly below the rotorhead. In forward flight, the center of mass will move aft to balance the negative pitch torque produced by applying cyclic control to propel the helicopter forward; consequently a cruising helicopter flies "nose-down" in level flight.
Astronomy
The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the barycenter. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star, both bodies are actually orbiting around a point that lies outside the center of the primary (the larger body).[26] For example, the moon does not orbit the exact center of the Earth, but a point on a line between the center of the Earth and the Moon, approximately 1,710 km (1062 miles) below the surface of the Earth, where their respective masses balance. This is the point about which the Earth and Moon orbit as they travel around the Sun.
See also
- Center of percussion
- Center of pressure
- Mass point geometry
- Metacentric height
- Roll center
- Weight distribution
References
- ^ Van Pelt 2005, p. 185.
- ^ a b c Kleppner & Kolenkow 1973, p. 117.
- ^ Kleppner & Kolenkow 1973, p. 119.
- ^ Levi 2009, p. 85.
- ^ Giambattista, Richardson & Richardson 2007, p. 235.
- ^ a b c Feynman, Leighton & Sands 1963, p. 19.3.
- ^ Kleppner & Kolenkow 1973, p. 116.
- ^ Kleppner & Kolenkow 1973, p. 262.
- ^ Kleppner & Kolenkow 1973, p. 252.
- ^ Goldstein, Poole & Safko 2001, p. 185.
- ^ Symon 1971, p. 260.
- ^ Shore 2008, pp. 9–11.
- ^ Baron 2004, pp. 91–94.
- ^ Baron 2004, pp. 94–96.
- ^ Baron 2004, pp. 96–101.
- ^ Baron 2004, pp. 101–106.
- ^ Mancosu 1999, pp. 56–61.
- ^ Walton 1855, p. 2.
- ^ Beatty 2006, p. 29.
- ^ Kleppner & Kolenkow 1973, pp. 119–120.
- ^ Feynman, Leighton & Sands 1963, pp. 19.1–19.2.
- ^ Hamill 2009, pp. 20–21.
- ^ Sangwin 2006, p. 7.
- ^ Federal Aviation Administration 2007, p. 1.4.
- ^ Federal Aviation Administration 2007, p. 1.3.
- ^ Murray & Dermott 1999, pp. 45–47.
- Baron, Margaret E. (2004) [1969], The Origins of the Infinitesimal Calculus, Courier Dover Publications, ISBN 0-486-49544-2
- Beatty, Millard F. (2006), Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Mathematical Concepts and Methods in Science and Engineering, 33, Springer, ISBN 0-387-23704-6
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1963), The Feynman Lectures on Physics, Addison Wesley, ISBN 0-201-02116-1
- Federal Aviation Administration (2007), Aircraft Weight and Balance Handbook, United States Government Printing Office, http://www.faa.gov/library/manuals/aircraft/media/FAA-H-8083-1A.pdf, retrieved 23 October 2011
- Giambattista, Alan; Richardson, Betty McCarthy; Richardson, Robert Coleman (2007), College physics, Volume 1 (2nd ed.), McGraw-Hill Higher Education, ISBN 0-071-10608-1, http://books.google.com/books?ei=qLuyTP6IL8OfOv6H6e0F
- Goldstein, Herbert; Poole, Charles; Safko, John (2001), Classical Mechanics (3rd ed.), Addison Wesley, ISBN 0-201-65702-3
- Hamill, Patrick (2009), Intermediate Dynamics, Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
- Kleppner, Daniel; Kolenkow, Robert (1973), An Introduction to Mechanics (2nd ed.), McGraw-Hill, ISBN 0-07-035048-5
- Levi, Mark (2009), The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press
- Mancosu, Paolo (1999), Philosophy of mathematics and mathematical practice in the seventeenth century, Oxford University Press, ISBN 0-19-513244-0
- Murray, Carl; Dermott, Stanley (1999), Solar System Dynamics, Cambridge University Press, ISBN 0-521-57295-9
- Sangwin, Christopher J. (2006), "Locating the centre of mass by mechanical means", Journal of the Oughtred Society 15 (2), http://web.mat.bham.ac.uk/C.J.Sangwin/Publications/integrometer.pdf, retrieved 23 October 2011
- Shore, Steven N. (2008), Forces in Physics: A Historical Perspective, Greenwood Press, ISBN 978-0-313-33303-3
- Symon, Keith R. (1971), Mechanics (3rd ed.), Addison-Wesley, ISBN 0-201-07391-7
- Van Pelt, Michael (2005), Space Tourism: Adventures in Earth Orbit and Beyond, Springer, ISBN 0387402136
- Walton, William (1855), A collection of problems in illustration of the principles of theoretical mechanics (2nd ed.), Deighton, Bell & Co., http://books.google.com/books?id=vY1NAAAAMAAJ
External links
- Motion of the Center of Mass shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
- The Solar System's barycenter Simulations showing the effect each planet contributes to the Solar System's barycenter
|
||||||||